

Statements Reasons 1) AB = DP ∠A = ∠D and AC = DQ 1) Given and by construction 2) ΔABC ≅ ΔDPQ 2) By SAS postulate 3) AB ACĭE DF 4) By substitution 5) PQ || EF 5) By converse of basic proportionality theorem 6) ∠DPQ = ∠E and ∠DQP = ∠F 6) Corresponding angles 7) ΔDPQ ~ ΔDEF 7) By AAA similarity 8) ΔABC ~ ΔDEF 8) From (2) and (7)ġ) In the given figure, if QT / PR = QR / QS and ∠1 = ∠2. Given : Two triangles ABC and DEF such that ∠A = ∠D AB ACĬonstruction : Let P and Q be two points on DE and DF respectively such that DP = AB and DQ = AC. There are three ways to find if two triangles are similar: AA, SAS and SSS: AA.

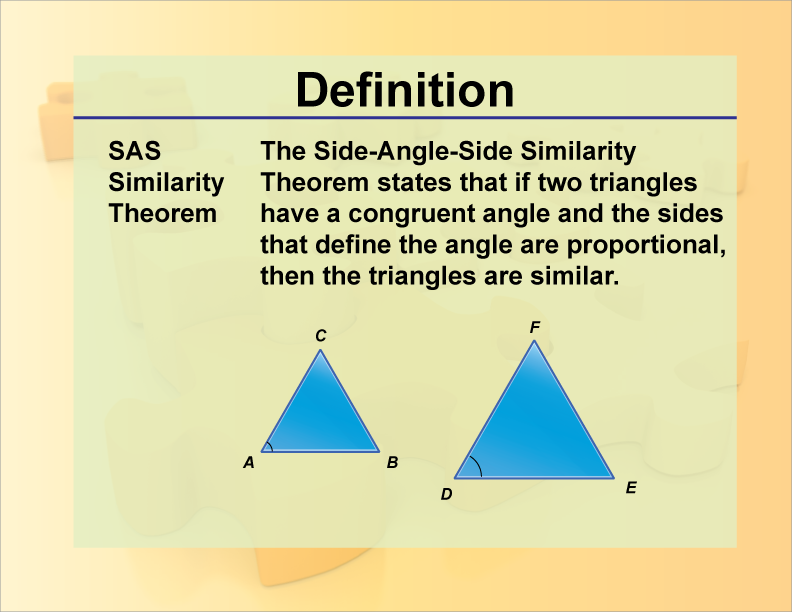
SAS Similarity SAS Similarity : If in two triangles, one pair of corresponding sides are proportional and the included angles are equal then the two triangles are similar. two or three out of the six is usually enough. This is called the SAS Similarity Theorem.


 0 kommentar(er)
0 kommentar(er)
